💡
Importante: Para entender esta resolución es
clave que primero hayas visto las clases de
estática de cuerpo extenso, donde resolvemos varios ejercicios de este estilo en video. Mi consejo es que veas
primero las clases y resoluciones que aparecen en esa sección y
después vengas a estos ejercicios de la guía, para seguir practicando.
Arrancamos primero haciendo un esquema de la situación, y ya te pongo abajo también cuál sería el diagrama del subibaja con las fuerzas que están actuando sobre él. Por cómo está planteado el enunciado, nos va a convenir elegir como centro de momentos el centro del subibaja (te lo marqué con la cruz naranja)
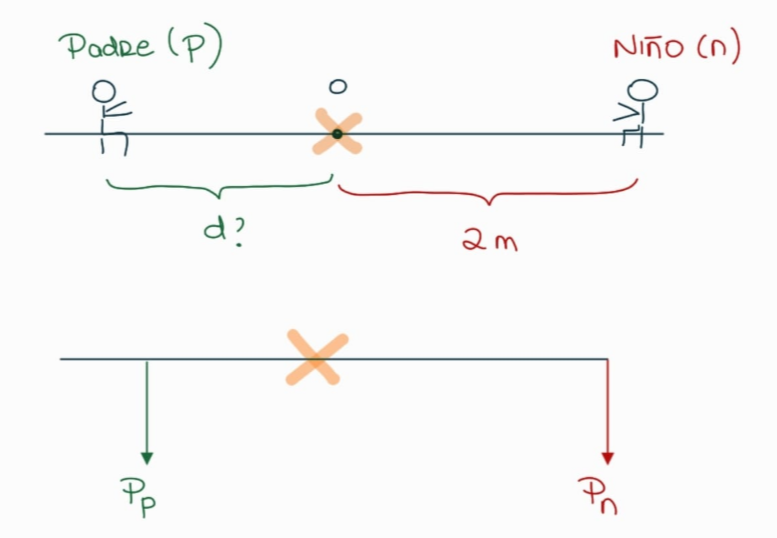
Respecto de nuestro centro de momentos $o$ calculamos el momento de la fuerza peso del niño $(P_n)$ y de la fuerza peso del padre $(P_p)$
👉 $|M_{P_n}| = d \cdot F_{\perp} = 2 \text{ m} \cdot P_n = 2 \text{ m} \cdot 21 \text{ kg} \cdot 9.8 \, \frac{m}{s^2} = 411.6 \text{ N} \cdot m$
Como esta fuerza me produce un giro en sentido horario, entonces le pongo signo negativo ➡️ $-411.6 \text{ N} \cdot m$
👉 $|M_{P_p}| = d \cdot F_{\perp} = d \cdot P_p = d \cdot 105 \text{ kg} \cdot 9.8 \, \frac{m}{s^2} = d \cdot 1029 \text{ N}$
Como esta fuerza me produce un giro en sentido antihorario, entonces le pongo signo positivo ➡️ $d \cdot 1029 \text{ N}$
Pedimos ahora que la suma de momentos respecto de $o$ sea cero, para que el subibaja esté en equilibrio:
$\sum M_{(o)} = 0$
$-411.6 \text{ N} \cdot m + d \cdot 1029 \text{ N} = 0$
Despejamos $d$
$d \cdot 1029 \text{ N} = 411.6 \text{ N} \cdot m$
$d = 0.4 \text{ m}$
Por lo tanto, el padre debe sentarse a $0.4$ metros del centro de giro para que el subibaja esté en equilibrio.

